Multiply mixed numbers
Multiply Mixed Numbers and Write in Lowest Terms
MULTIPLY MIXED NUMBERS INSTRUCTIONS
Follow the directions in the dialog box after pressing the <START> button. The <EXPLAIN> button may be pressed after you enter the second factor to see how to do the example.
The following image was made from Multiply Fractions with Lines Designer:
Multiply Fractions-Strict is similar to the previous program MULTIPLY FRACTIONS except that both factors may be mixed numbers and the product must be written as a mixed number or whole number and in lowest terms.
See the program MIXED NUMBERS for information on writing fractions in mixed number form.
See the program RENAME IN LOWEST TERMS for information on writing fractions in lowest terms.
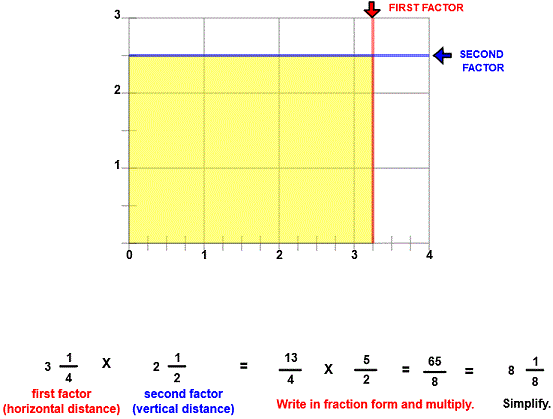
The above image shows six whole units.There are also three 1⁄2 units, two 1⁄4 units and one 1⁄8 unit. This all adds up to the product of 81⁄8 units.
You can see from the picture that the first factor is 31⁄4 units in length and the second factor is 2 1⁄2 units in length. To calculate the product, first write each factor in fraction form. Then multiply the numerators of each factor for the numerator of the product and the denominators of each factor for the denominator of the product.
When the program starts, you will be asked to identify the first factor and then the second factor. You will then be asked to find the product.
How to Cancel will play a short animation that demonstrates this shortcut way to write a fraction in lowest terms.
For more instruction on multiplying fractions go to How To Multiply Fractions.
After you enter the product you may press the <REPORT> button. The report will ask for your name but you may submit a code for your name. This report will give same results as on the dialog box. The report may be printed or e-mailed.
