Compare fractions with circle models
Circle models show show how to compare unlike fractions using a common denominator.
COMPARE FRACTIONS WITH CIRCLE MODELS INSTRUCTIONS
Follow the directions in the dialog box after pressing the <START> button. The <EXPLAIN> button may be pressed to see how to do the example.
When Compare Fractions starts, you will be given two fractions to compare, as in the example below:

You are to decide if the fraction on the left is less than, equal to, or greater than the fraction on the right. You will choose < for less than, = for equal to, or > for greater than. Shown in the dialog box are your choices of <, >, or =.
If the denominators are the same, the fraction with the larger numerator is larger and if the numerators are the same, the fraction with the larger denominator is smaller.
The following compare fractions illustration was made by Compare Fractions With Circles Designer:
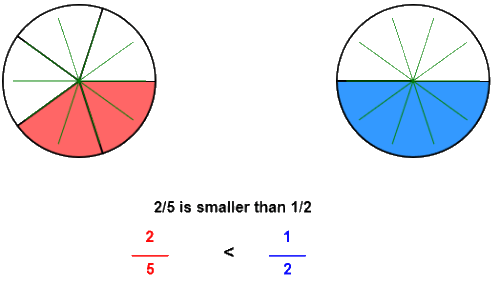
The fractions 2⁄5 and 1⁄2 are pictured below:
Let's make the denominators the same so that we can compare the numerators. Fractions with the same denominators are like fractions.
Here, we will introduce the idea of the least common denominator or LCD. LCD is an idea that will be used in comparing, adding, and subtracting fractions. The LCD is the smallest number that both 5 and 2 will divide into evenly. Ten is the LCD for the fractions 2⁄5 and 1⁄ 2 because both denominators 5 and 2 divide evenly into 10.;
Once the LCD is found, each fraction is written with the LCD. As you can see by the illustration, 2⁄5 is equal to 4⁄10 and 1⁄ 2 is equal to 5⁄10. Once each fraction is renamed with a common denominator, you only have to compare the numerators. The larger the numerator the larger the fraction.
See the program RENAME IN HIGHER TERMS for more information on renaming fractions.
One way to determine the LCD is to see if the smaller denominator 2 will divide evenly into the larger denominator 5. If not, multiply the larger denominator by 2 to get 10. Will the smaller denominator 5 divide into 10? Yes, so 10 is the LCD. If not, multiply the larger denominator by 3, then 4, etc. until the smaller denominator divides into the product.
Another method is to multiply the two denominators and then divide that product by the greatest common factor(GCF) of the two denominators. The greatest common factor is the largest number that will divide evenly into the two denominators. In the example above the GCF of 5 and 2 is 1. The product of 5 and 2 is 10. Divide 10 by 1 and you get 10 for the LCD.
Also, you can see that 2⁄5 is less than half the circle so 2⁄5 is smaller.
Choose the < (less than) button if you think the first fraction is smaller than the second. Choose the = (equal button) if you think the two fractions are the same size. Choose the > (greater than) if you think
the fraction is larger. If correct, circles showing the comparative sizes of the two fractions will appear. Press the <EXPLAIN> button to see each fraction with the common denominator.
For more instruction on comparng fractions go to How To Compare Fractions.
After you press the <, =, or > button you may press the <REPORT> button. The report will ask for your name but you may submit a code for your name. This report will give same results as on the dialog box. The report may be printed or e-mailed.
